grafica de función racional

Función racional

Las funciones racionales son del tipo:

El dominio de una función racional de lo forman todos los números reales menos los valores de x que anulan el denominador.

Ejemplo

Un tipo de función racional es la función de proporcionalidad inversa de ecuación:

  .

Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones   

Construcción de hipérbolas

Las hipérbolas   son las más sencillas de representar.

Sus asítontas son los ejes

El centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen.

A partir de estas hipérbolas se obtienen otras por traslación.

1. Traslación vertical

El centro de la hipérbola es: (0, a).

Si a>0, se desplaza hacia arriba a unidades.

El centro de la hipérbola es: (0, 3)

Si a<0, se desplaza hacia abajo a unidades.

El centro de la hipérbola es: (0, -3)

2. Traslación horizontal

El centro de la hipérbola es: (-b, 0).

Si b> 0, se desplaza a la izquierda b unidades.

El centro de la hipérbola es: (-3, 0)

Si b<0, se desplaza a la derecha b unidades.

El centro de la hipérbola es: (3, 0)

3. Traslación oblicua

El centro de la hipérbola es: (-b, a)

El centro de la hipérbola es: (3, 4).

Para representar hipérbolas del tipo:

se divide y se escribe como:

Su representación gráfica es una hipérbola de centro (-b, a) y de asíntotas paralelas a los ejes.

El centro de la hipérbola es: (-1, 3)

función racional

Guía función racional from Sara Petricorena

teorema de factorización

Para entender la operación algebraica llamada factorización es preciso repasar los siguientes conceptos:
Cualquier expresión que incluya la relación de igualdad (=) se llama ecuación.
Una ecuación se denomina identidad si la igualdad se cumple para cualquier valor de las variables; si la ecuación se cumple para ciertos valores de las variables pero no para otros, la ecuación es condicional.
Un término es una expresión algebraica que sólo contiene productos de constantes y variables; 2x, – a, 3x son algunos ejemplos de términos.
La parte numérica de un término se denomina coeficiente.
Los coeficientes de cada uno de los ejemplos anteriores son 2, – 1, y 3.
Una expresión que contiene un solo término se denomina monomio; si contiene dos términos se llama binomio y si contiene tres términos, es un trinomio.
Un polinomio es una suma (o diferencia) finita de términos.
En este contexto, el grado es el mayor exponente de las variables en un polinomio. Por ejemplo, si el mayor exponente de la variable es 3, como en ax³ + bx² + cx, el polinomio es de tercer grado.
Una ecuación lineal en una variable es una ecuación polinómica de primer grado; es decir, una ecuación de la forma ax + b = 0.
Se les llama ecuaciones lineales porque representan la fórmula de una línea recta en la geometría analítica.
Una ecuación cuadrática en una variable es una ecuación polinómica de segundo grado, es decir, de la forma ax² + bx + c = 0.
Un número primo es un entero (número natural) que sólo se puede dividir exactamente por sí mismo y por 1. Así, 2, 3, 5, 7, 11 y 13 son todos números primos.
Las potencias de un número se obtienen mediante sucesivas multiplicaciones del número por sí mismo. El término a elevado a la tercera potencia, por ejemplo, se puede expresar como a·a·a o a³
Los factores primos de un cierto número son aquellos factores en los que éste se puede descomponer de manera que el número se puede expresar sólo como el producto de números primos y sus potencias.

Descomposición de números naturales en sus factores primos

Por ejemplo, un número natural como 20 puede expresarse como un producto de números de diferentes formas:

20 = 2 • 10 = 1 • 20 = 4 • 5

En cada uno de estos casos, los números que forman el producto son los factores.
Es decir, cuando expresamos el número 20 como el producto 2 • 10, a cada uno de los números (2 y 10) se les denomina factor.
En el caso de 1 • 20 los factores son 1 y 20 y finalmente en el caso de 4 • 5, los factores son 4 y 5.
Cada uno de los números 1, 2, 4, 5, 10, 20 se denominan a su vez divisores de 20.
Otro ejemplo, los factores primos de 15 son 3 y 5. Del mismo modo, como 60 = 2² • 3 • 5, los factores primos de 60 son 2, 3 y 5.
Debe recordarse, además, que cuando un número es divisible únicamente por sí mismo y por la unidad el número se denomina primo.

Factorización y productos notables

Así como los números naturales pueden ser expresados como producto de dos o más números, los polinomios pueden ser expresadas como el producto de dos o más factores algebraicos.
Cuando un polinomio no se puede factorizar se denomina irreducible. En los casos en que la expresión es irreducible, solo puede expresarse como el producto del número 1 por la expresión original.
Al proceso de expresar un polinomio como un producto de factores se le denomina factorización.
El proceso de factorización puede considerarse como inverso al proceso de multiplicar.
Factorizar, entonces, quiere decir identificar los factores comunes a todos los términos y agruparlos.
Los factores comunes son aquellos números que aparecen multiplicando a todos los términos de una expresión algebraica.
Estos números pueden estar dados explícitamente o representados por letras.
Así, factorizar un polinomio es descomponerlo en dos o más polinomios llamados factores, de tal modo que al multiplicarlos entre sí se obtenga el polinomio original.
En otras palabras, dada una expresión algebraica complicada, resulta útil, por lo general, el descomponerla en un producto de varios términos más sencillos.
Por ejemplo, 2x³ + 8x²y se puede factorizar, o reescribir, como 2x²(x + 4y).
Algunos ejemplos:
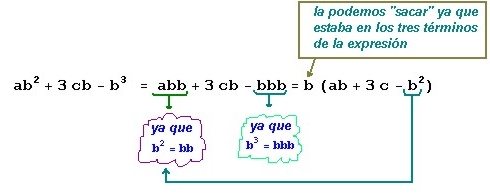
De la expresión    ab² + 3cb - b³ podemos factorizar  b
y obtenemos la expresión:   b(ab + 3c - b²) (1)
Veamos paso a paso cómo se obtuvo la expresión:

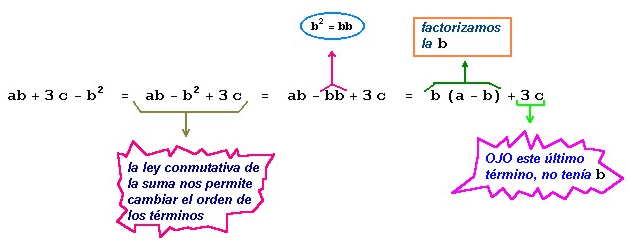
ahora podríamos reacomodar la expresión que queda dentro del paréntesis:

Finalmente si sustituimos este último resultado en (1), obtenemos:

ab² + 3cb - b³ = b (b (a - b) + 3c)

ab² + 3cb - b³ = b (ab - b² + 3c)

ab² + 3cb - b³ = b (ab +3c –b²)

Por otro lado, algunos productos sencillos que tienen una estructura determinada y que pueden ser evaluados de forma directa se denominan Productos notables.
En general los casos de factorización corresponden a los casos de productos notables.
Antes de mostrar ejercicios de aplicación de factorización y productos notables, es necesario recordar la forma de hallar el máximo común divisor (mcd) de un conjunto de números dados.
Ejemplo: Determinar el máximo común divisor (mcd) de los números 56, 42 y 28.
El máximo común divisor de un conjunto de números dados corresponde al mayor número natural que los divide simultáneamente, con residuo cero.
Para hallar el mcd de un conjunto determinado de números, estos se dividen simultáneamente por los diferentes números primos (tomados en orden ascendente, y desechando los números primos por los cuales no se pueda hacer la división con residuo cero de todos los números de la fila) según el arreglo mostrado a continuación.
El proceso termina, cuando los números que aparecen en la fila inmediatamente inferior a la última división simultánea, no pueden dividirse simultáneamente por algún número primo.
El mcd buscado es el producto de los números primos que aparecen a la derecha:

56	42	28	÷	2
28	21	14	÷	7
4	3	2

Los números originales (56, 42, 28) se escriben desde la izquierda hacia la derecha.
A la derecha de ellos se escribe el 2 (primer número primo de la lista) y se divide cada uno de estos números por 2, escribiendo el resultado obtenido en la misma columna del número original.
La segunda fila muestra estos resultados.
Como los números 28, 21 y 14 no pueden dividirse simultáneamente por 3, este número primo se desecha.
De forma similar se desecha el 5.
El siguiente número primo en la lista es 7.
En este caso se puede hacer la división simultáneamente obteniéndose los números 4, 3 y 2.
Esta última fila no puede dividirse simultáneamente ni por 2 ni por 3.
Como el siguiente número primo (5) es mayor que 4, el proceso termina.
Por lo tanto, el mcd de los números 56, 42 y 28 es el producto de los números primos de la derecha: 2 • 7 = 14
Lo anterior se expresa como: mcd (56, 42, 28) = 14  (el máximo común divisor de los números 56, 42 y 28 es igual a 14)
Ejemplo: Factorizar  9x + 6y - 12z
Este es un ejemplo sencillo de la factorización por factor común.
Dada una expresión algebraica se encuentra el máximo común divisor (mcd) de los coeficientes de los términos de la expresión algebraica.
Este mcd corresponde al coeficiente del factor común.
Para la parte literal se toman las variables comunes a todos los términos con el menor exponente que aparezca.
Para este ejercicio el mcd de 9, 6 y 12 es 3; además como no hay variables comunes en los tres términos tenemos:

9x + 6y - 12z = 3(3x + 2y - 4z)

es decir 9x  + 6y - 12z se ha expresado como el producto de los factores 3 y 3x + 2y - 4z.
Ejemplo: Factorizar  9xy² + 6y⁴ - 12 y³z
En este caso además del factor común 3 (mcd de 9, 6, 12) la variable y es común a los tres términos. La menor potencia común es  y² por lo tanto la factorización queda:

9xy² + 6y⁴ - 12y³z = 3y²(3x + 2y² - 4yz)

Los factores en este caso son 3x + 2y² - 4yz  y  3y². Para verificar, al realizar el producto indicado se obtiene la expresión original:

3y²(3x + 2y² - 4yz) = (3y² * 3x) + (3y² * 2y²) - (3y² * 4yz)

= 9xy² + 6y⁴ - 12y³z

Nótese que se ha aplicado la propiedad distributiva del producto. En general no es necesario hacer la verificación de la factorización, pero es conveniente cuando existan dudas sobre el resultado obtenido:

teorema fundamental del algebra

Análisis del teorema fundamental del álgebra.

Teorema fundamental del álgebra. Un polinomio de grado n impar admite al menos una raíz real. Si existe una raíz compleja  de un polinomio, entonces existe su raíz compleja conjugada .

Este teorema resulta de suma importancia dentro del estudio de las ecuaciones. Encontrar la solución de una ecuación representa encontrar todos los valores de x para los cuales la ecuación  es cierta, a las que comúnmente le llamamos raíces de la ecuación, generalmente las soluciones que de manera inmediata nos interesan son los valores que existan en los reales, sin que con ello las soluciones complejas no sean interesantes.

La obtención de soluciones de una ecuación tiene un sentido gráfico que nos es de particular interés. En el caso particular en que las soluciones sean reales estas representan los puntos de intersección con el eje x.

Ejemplo:

 

Encuentre la solución de la siguiente ecuación .

 

Comentamos que encontrar la solución de una ecuación es encontrar los valores de x reales para los cuales ,  es decir, en este caso si hacemos y(x)=0 tendremos

Vemos que este es el único valor para el cual , es decir, solo existe una raíz, algo que era un resultado que podíamos afirmar del teorema fundamental del álgebra, si el polinomio es de grado impar por lo menos tenemos una raíz real, en este caso como el polinomio es de primer grado era lógico suponer que no existía mas de una sola solución o raíz. Su aspecto gráfico es el siguiente, el punto de intersección con el eje x es   cuando y=0. La gráfica de la ecuación es una línea recta de pendiente 2 ya que recordando la ecuación de la línea recta de la forma  con m la pendiente.  La ordenada al origen es b=1 es decir con ello tenemos la otra coordenada que se requiere para representar una línea recta, .

 

 

Abordemos ahora las ecuaciones de segundo grado, las posibilidades que tenemos para dichas ecuaciones son las siguientes: a).- raíces iguales y en forma gráfica solo tocara al eje x una sola vez, por supuesto que las raíces son reales,  b).- raíces diferentes y reales, el gráfico de dicha ecuación interfecta en dos puntos al eje x,  c).- las raíces son complejas y el gráfico jamás cruzara al eje de las x

De hecho podemos generalizar el ejemplo presentado y asegurar que la ecuación del tipo , con a positivo,  representa una familia de parábolas, cuya intersección con el eje x se da una sola vez. Si se toma el signo positivo se tiene una familia de parábolas con intersección con el eje x negativo, por el contrario, si tomamos el signo negativo tendremos la intersección con el eje x positivo.

 

Analizando el inciso b), raíces diferentes y reales, el gráfico de dicha ecuación interfecta en dos puntos al eje x , ejemplo de dicha ecuación tenemos, las expresiones cuadráticas que se pueden acomodar de la forma  es decir admite una factorización, generalizando podremos observar que un aspecto importante de la factorización para polinomios radica en la obtención de raíces, esto como consecuencia del teorema fundamental del álgebra

 

Un ejemplo de esta expresión es el siguiente binomio, , el cual tiene raíces , es decir, se factoriza de la siguiente forma . El gráfico de dicha ecuación es dada como:

 

Otro ejemplo lo tendríamos, con la siguiente ecuación:  cuyas raíces son , en consecuencia podemos expresar la ecuación de la forma

 

 

 

el último caso es cuando la ecuación no se puede descomponer en factores, no se tienen raíces en los reales y por lo tanto no cruza el gráfico al eje x.

 

 

por ejemplo la expresión siguiente es una ecuación que no tiene raíces en el campo de las x, , podemos extender este caso y garantizar que todas las ecuaciones de la forma , con a positivo, no tienen raíces reales ni intersectan al eje de las x. En particular el gráfico para la ecuación  es dado como: