Una
función cuadrática es aquella que puede escribirse como una ecuación de la forma:
f(x) = ax2 + bx + c
donde
a,
b y
c (llamados
términos) son números reales cualesquiera y
a es distinto de
cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de
b y de
c sí puede ser
cero.
En la ecuación cuadrática cada uno de sus términos tiene un nombre.
Así,
ax2 es el término
cuadrático
bx es el término
lineal
c es el término
independiente
Cuando estudiamos la
ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es un
ecuación completa, si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es
incompleta.
Representación gráfica de una función cuadrática
Si pudiésemos representar en una gráfica "todos" los puntos
[x,f(x)] de una
función cuadrática, obtendríamos siempre una curva llamada
parábola.
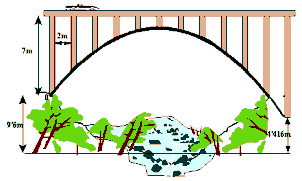 |
| Parábola del puente, una función cuadrática. |
Como contrapartida, diremos que una
parábola es la representación gráfica de una
función cuadrática.
Dicha parábola tendrá algunas características o elementos bien
definidos dependiendo de los valores de la ecuación que la generan.
Estas características o elementos son:
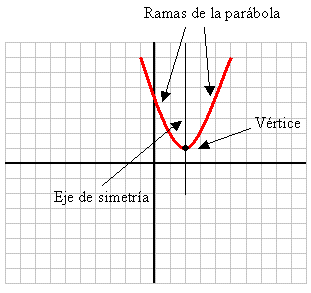
Orientación o concavidad (ramas o brazos)
Puntos de corte con el eje de abscisas (raíces)
Punto de corte con el eje de ordenadas
Eje de simetría
Vértice
Orientación o concavidad
Una primera característica es la
orientación o
concavidad de la parábola. Hablamos de
parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de
parábola convexa si sus ramas o brazos se orientan hacia abajo.
Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático
(la ax2):
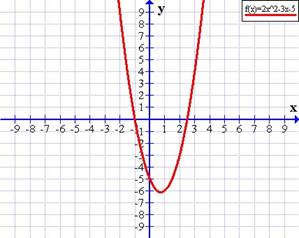
Si a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2 − 3x − 5
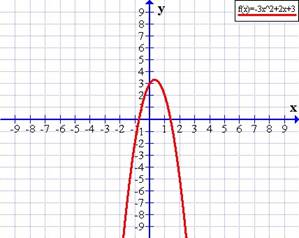
Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3
Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.
Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)
Otra característica o elemento fundamental para graficar una función cuadrática la da el valor o los valores que adquiera x, los cuales deben calcularse.
Ahora, para calcular las raíces (soluciones) de cualquier función cuadrática calculamos
f (x) = 0.
Esto significa que las raíces (soluciones) de una función cuadrática son aquellos valores de x para los cuales la expresión vale 0; es decir, los valores de x tales que y = 0; que es lo mismo que f(x) = 0.
Entonces hacemos
ax² + bx +c = 0
Como la ecuación ax² + bx +c = 0 posee un
término de segundo grado, otro de primer grado y un término constante,
no podemos aplicar las propiedades de las ecuaciones, entonces, para
resolverla usamos la fórmula:
Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas).
Respecto a esta intersección, se pueden dar tres casos:
Que corte al eje X en dos puntos distintos
Que corte al eje X en un solo punto (es tangente al eje x)
Que no corte al eje X
Esta característica se puede determinar analizando el discriminante, ya visto en las ecuaciones cuadráticas.
Punto de corte en el eje de las ordenadas (eje de las Y)
En el eje de ordenadas (Y) la primera coordenada es cero, por lo que el punto de corte en el eje de las ordenadas lo marca el valor de c (0, c).
Veamos:
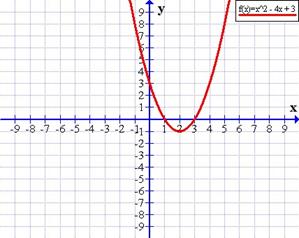
Representar la función f(x) = x² − 4x + 3
El eje de las ordenadas (Y) está cortado en +3
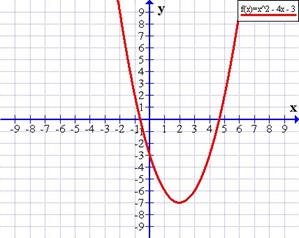
Representar la función
f(x) = x² − 4x − 3
El eje de las ordenadas (Y) está cortado en −3
Observar que la parábola siempre cortará al eje de las ordenadas (Y),
pero como ya vimos más arriba al eje de abscisas (X) puede que no lo
corte, lo corte en dos puntos o solamente en uno.
Eje de simetría o simetría
Otra característica o elemento de la parábola es su
eje de simetría.
El
eje de simetría de una parábola es una recta vertical que
divide simétricamente a la curva; es decir, intuitivamente la separa en
dos partes congruentes. Se puede imaginar como un espejo que refleja
la mitad de la parábola.
Su ecuación está dada por:
Donde
x1 y
x2 son las raíces de la ecuación de segundo grado en
x, asociada a la parábola.
De aquí podemos establecer la
ecuación del eje de simetría de la parábola:
Vértice
Como podemos ver en gráfico precedente, el
vértice de la parábola es el punto de corte (o punto de intersección) del eje de simetría con la parábola y tiene como coordenadas
La abscisa de este punto corresponde al valor del eje de simetría
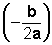
y la ordenada corresponde al valor máximo o mínimo de la función,
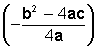
según sea la orientación de la parábola (recuerde el
discriminante)


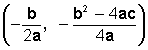
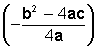 según sea la orientación de la parábola (recuerde el discriminante)
según sea la orientación de la parábola (recuerde el discriminante)












